Decoding planetary surfaces by counting cracks
Sophie Silver, Douglas Jerolmack, Krisztina Regős, Gábor Domokos.
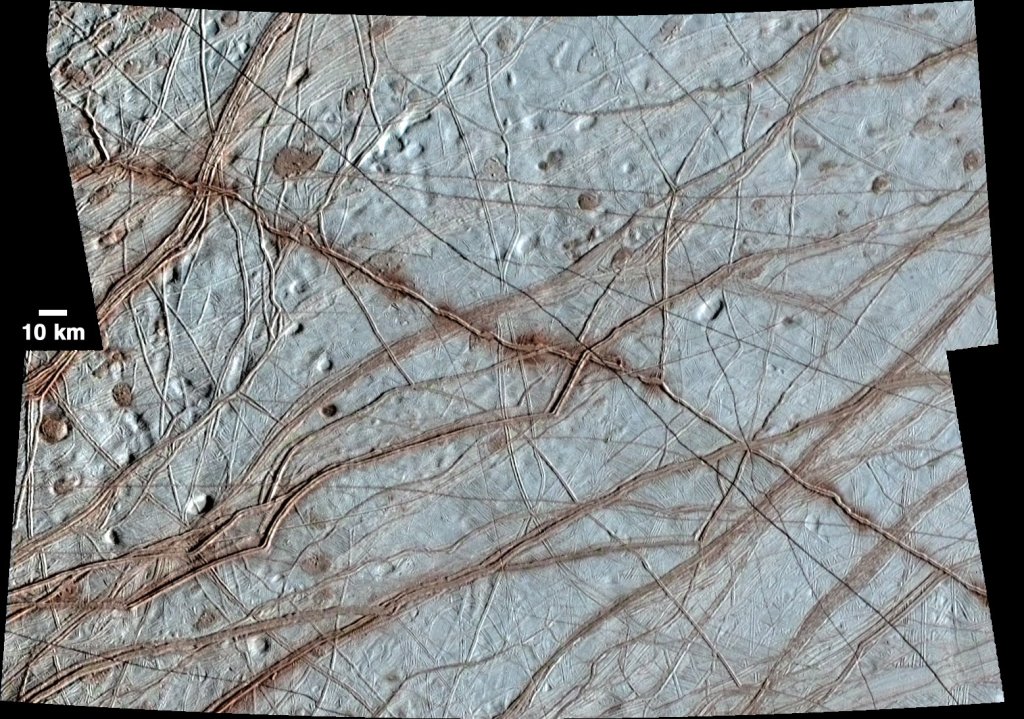
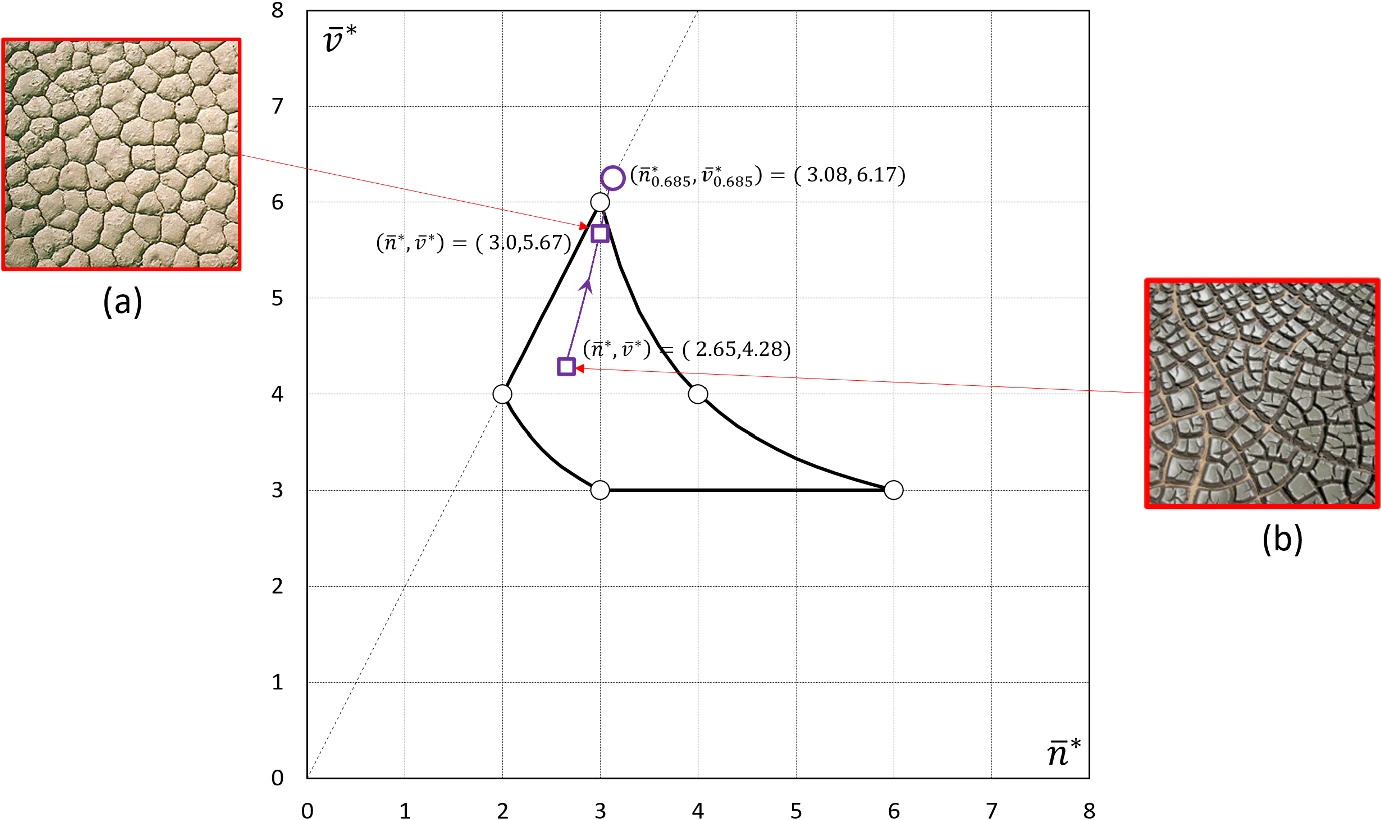
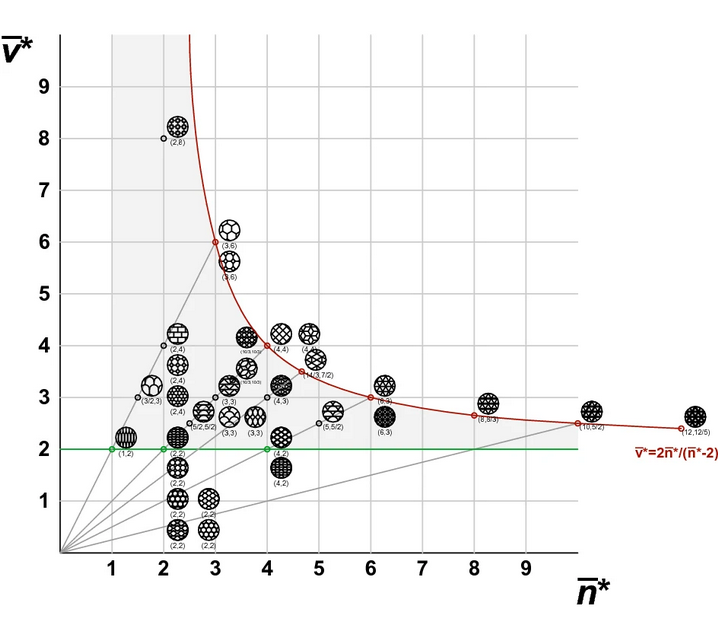
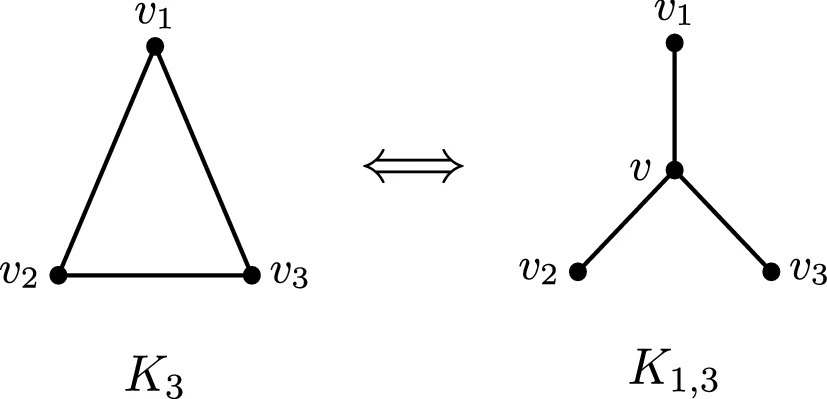
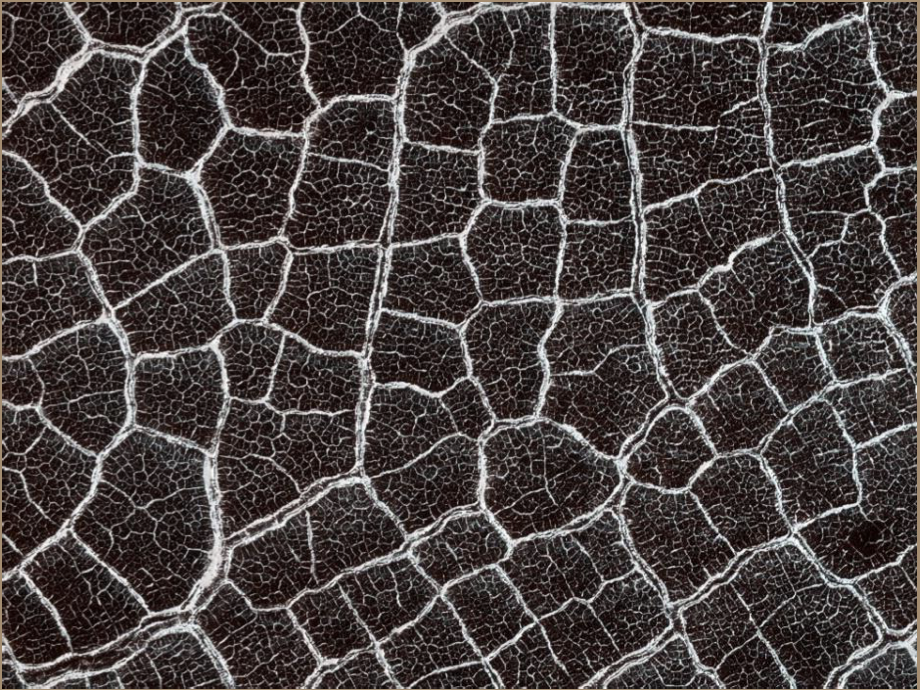
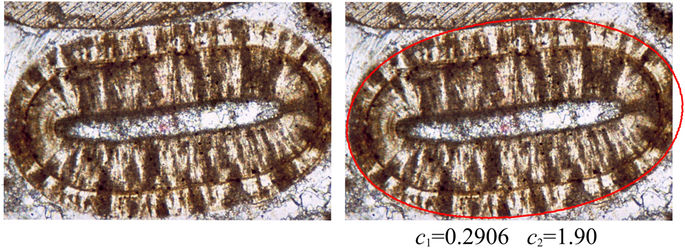
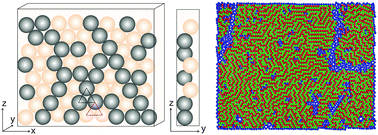
Abstract: Planets are often covered with thin cracked shells. From mud films to lithospheres of rock or ice, fracture networks form two-dimensional (2D) tessellations of convex polygons whose geometry encodes their genesis. Here, we chart the geometry of 2D fracture mosaics across the solar system, and decode their formative conditions using a new dynamical crack model. We show that mosaics can be projected onto a Symbolic Ternary Diagram, where the relative proportions of “T,” “X,” and “Y” junctions are uniquely related to contributions from distinct modes of fracture. Most planetary mosaics cluster in a region associated with hierarchical fracture networks, where sequential cracking favors formation of T junctions. Exceptions to this rule may betray the presence of water. Europa’s fracture networks stand apart due to the predominance of X junctions; this is a special feature of ice, where healing of cracks by refreezing of water allows new fractures to overprint older ones. Several fracture networks on Mars appear as outliers due to the high proportion of Y junctions. These patterns—previously interpreted as ancient mudcracks and frozen polar terrain, based on geological evidence—are consistent with the twisting of crack junctions by cyclic volume change. Our findings suggest that counting cracks could aid in the identification of other water-influenced planetary environments.
(See also the related interview at the website of BME.)