An Evolution Model for Polygonal Tessellations as Models for Crack Networks and Other Natural Patterns
Péter Bálint, Gábor Domokos, Krisztina Regős.
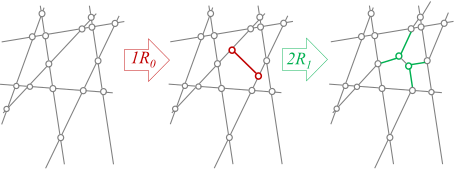
Abstract: We introduce and study a general framework for modeling the evolution of crack networks. The evolution steps are triggered by exponential clocks corresponding to local micro-events, and thus reflect the state of the pattern. In an appropriate simultaneous limit of pattern domain tending to infinity and time step tending to zero, a continuous time model, specifically a system of ODE is derived that describes the dynamics of averaged quantities. In comparison with the previous, discrete time model, studied recently by two of the present three authors, this approach has several advantages. In particular, the emergence of non-physical solutions characteristic to the discrete time model is ruled out in the relevant nonlinear version of the new model. We also comment on the possibilities of studying further types of pattern formation phenomena based on the introduced general framework.