Conway’s Spiral and a Discrete Gömböc with 21 Point Masses
Gábor Domokos, Flórián Kovács.
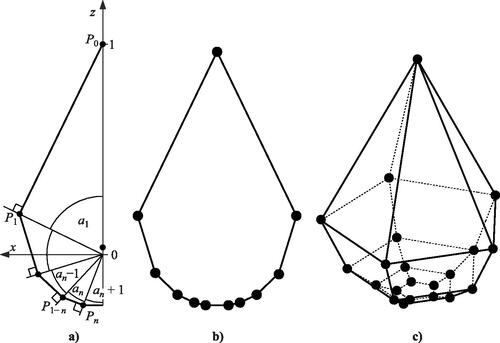
Abstract: We show an explicit construction in three dimensions for a convex, mono-monostatic polyhedron (i.e., having exactly one stable and one unstable equilibrium) with 21 vertices and 21 faces. This polyhedron is a 0-skeleton, with equal masses located at each vertex. The above construction serves as an upper bound for the minimal number of faces and vertices of mono-monostatic 0-skeletons and complements the recently provided lower bound of 8 vertices. This is the first known construction of a mono-monostatic polyhedral solid. We also show that a similar construction for homogeneous distribution of mass cannot result in a mono-monostatic solid.