At this year’s Student Research Conference 4 presentations were related to Morphodynamics: Adria Kerekes & Dávid Büki (1st Prize), Dániel Csallóközi (2nd Prize), Julia Hegymegi (3rd Prize), Menyhért Gergye (3rd Prize + Best presentation award).
1st Prize
Morphological analysis of fractured rock surfaces
Adria Flóra Kerekes, Dávid Büki
supervisor: Gábor Domokos
The goal of our Thesis is the continuation of our morphological research about fractures in the rock surface started in 2016. In the preceding paper, we applied the methods, which the Department of Mechanics, Materials & Structures has been using in their analysis for years to uncover unique geometrical characteristics, on surface cracks, observing two-dimensional patterns.
Continuing, we collected quasi 500 fragments from the same location, the top
of ’Hármashatárhegy’ at Budapest (latitude 47° 33′ N, longitude 18° 59′ E), which are presumably the products of the cracking process in our previous examination. Although these
are three-dimensional samples, by choosing appropriate shape parameters, the results are comparable to that of the two dimensional’.

During our work, we manually checked the mass (m), axis (a>b>c), stable (S) and unstable (U) equilibrium of every fragment. From the Department, we received a similar, separate (measured in the same manner) set of data. One of our Thesis’ theme is the statistical analysis of the differences between the two, from which we can draw general conclusions concerning the measurements. These are notably intriguing when it comes to S and U.
From the values, we calculated the axial ratio ( r=b/a ) then after the proper averaging with respect to the mass, we drew the r(m) graph, which we compared to our own, previous results of the two-dimensional contours and the [1] article’s results.
The three curves did not match, however after implementing and running the [1] article’s fragmentation model on the measurement results, we came to the conclusion, that the curves possibly show the consecutive states of the same fragmentation process, the first state being the cracked rock, then the fragment, which broke out and fragmented, lastly the universal mass-ratio correlation, which according to [1] article, defines every sufficiently long fragmentation process. To our knowledge, this is the first case of a successful morphological evaluation of the same processes two different states.
2nd Prize
Study and Visualisation of Distance-driven shape evolution models
Dániel Csallóközi
supervisor: Gábor Domokos
The first known mathematical model about pebble shape originates from Aristotle. He observed that the velocity of abrasion at a given P surface point of the pebble is a monotonically increasing function of the distance between the point P and geometric centre point S. From this observation, he concluded that the shape of such pebbles approaches an orb in the process of abrasion.
Converting Aristotle’s model into modern mathematics, we get a so-called distance-driven shape evolution model, of which we can prove that under certain circumstances it actually abrades pebbles towards an orb. The task of my study is to visualise the 3-dimensional version of this model. Within this context I analyse alteration of formal characteristics through the process, such as axle ratios of the bounding cuboid, isoperimetric ratio and the number of static equilibria. I also analyse one possible generalisation of the Aristotle-model, where the velocity of abrasion is not only function of the distance, but function of the first (spatial) derivatives of it also. In this study, I use (symmetric) figures, the geometric centre points of which stay permanent in the process of abrasion.
Programs form part of my study, which analyse and visualise the process of abrasion under the given circumstances, evaluate and depict the described formal characteristics and their alteration through the process. Figures attached to the study are results of these programs.
Creating this study, I used parts of curriculum of the optional subject “Mathematical Modelling of Mechanical Problems”.
3rd Prize
Sand in Hand
Julia Hegymegi
supervisor: Gábor Domokos, Eszter Fehér
During the summer of 2017 I have spent two months in the UK, working in a children’s holiday camp. This was not just my first time being abroad for a longer period, but also my first time getting closer to nature on a scientific basis. Observing sand on the shore was a new, and unique experience for me.
I collected sand at Salfleetby Theddlethorpe National Nature Reserve from 13 different locations along a perpendicular line to the coast. The samples were analysed individually.
1. photos of the grains were taken with a camera attached to a microscope,
2. with a MATLAB software provided by the Department of Mechanics, Materials and Structures geometric data from their contours were obtained.
These geometric data included surface area (A), convexity (c), isoperimetric ratio (I) and axis ratio (R).
What made us curious is that the mean value of the ir and the ar almost equalled to each other at all the sampling locations. The main goal of my research was to explore this phenomenon with mathematical and geomorphological tools.
A simplified, planar fragmentation model operating by splitting convex polygons into two parts by random straight lines shows that, regardless of the initial shape, after sufficiently many fragmentation events the average value of vertices (and edges) approaches 4. One may, based on this simple model say that natural (planar) fragments tend to be quadrangles.
I have also examined the evolution I(l) and R(l) in case of a twice (D2) symmetric convex shape S being transformed under linear affinity with parameter l, parallel to one of the symmetry axes. Apparently, for arbitrary S there exist two values l1≤l2 where R(li)=I(li) and l1=l2 holds only if S is an ellipse. Conveniently, we can set l=1 for R=1 allowing to compare the l1, l2 values for various shapes. Quite remarkably, we find that l1 reaches its minima on rectangles (l1=0.7724) and the rhombus (l1=0.7555) which are the only two quadrangles in this class. Additionally we find that the common I=R value for the measured fragments is in this range (0,774-0,778).
Guided by this mathematical discovery we had a closer look at the grain contours and we found that indeed most of them can be well approximated by slightly elongated rectangles.
This observation not only suggests that there may be indeed a relation between these mathematical models and the behaviour of Nature experienced on the coast but also offers a beautiful example where field work and mathematical reasoning go hand in sand.

3rd Prize + Best presentation award
Twofold Focus
Menyhért Gergye
supervisor: Gábor Domokos
“The triaxial ellipsoid shape can be often observed on stones at the places of undertow, along the seacoast. Any arbitrary shaped stone will slowly develope into an ellipsoid-like shape because of the abrasive work of water.”
-David Hilbert, Stefan Cohn-Vossen: Geometry and Imagination
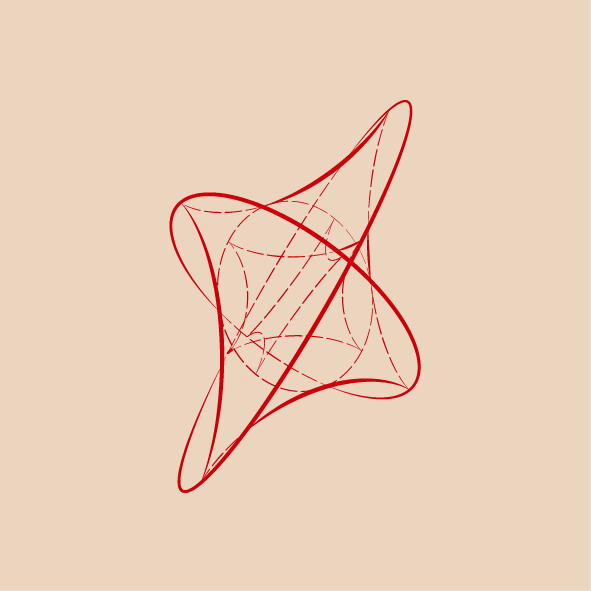
This quote’s author is one of the most influential mathematicians of the early 20th centuries, Professor of Mathematics at the University of Göttingen. His world-famous book, “Geometry and Imagination” testifies that according to Hilbert, the triaxial ellipsoid is the
way not only to the basics of differential geometry, but also to understand the shapes of nature. It is therefore surprising that if someone would like to find one of the most interesting geometrical object related to the triaxial ellipsoid, it’s focal surface (curvature centre point surface), the only available source is from the Göttingen Collection of Mathematical Models, a gypsum model numbered 240.The purpose of my essay is to construct this remarkable surface using the program GeoGebra and the Monge’s Method of Projections. For this I had to trace back the ellipsoid to it’s “thread” construction, locate it’s four umbilic points, find the directions of principal curvatures at a general point, and construct it’s confocal surfaces through that point. The construction of the curves of the focal surface in its plane of symmetry, and two points, belonging to one genereal point of the ellipsoid.