Month: December 2022

A discrete time evolution model for fracture networks
Gábor Domokos, Krisztina Regős

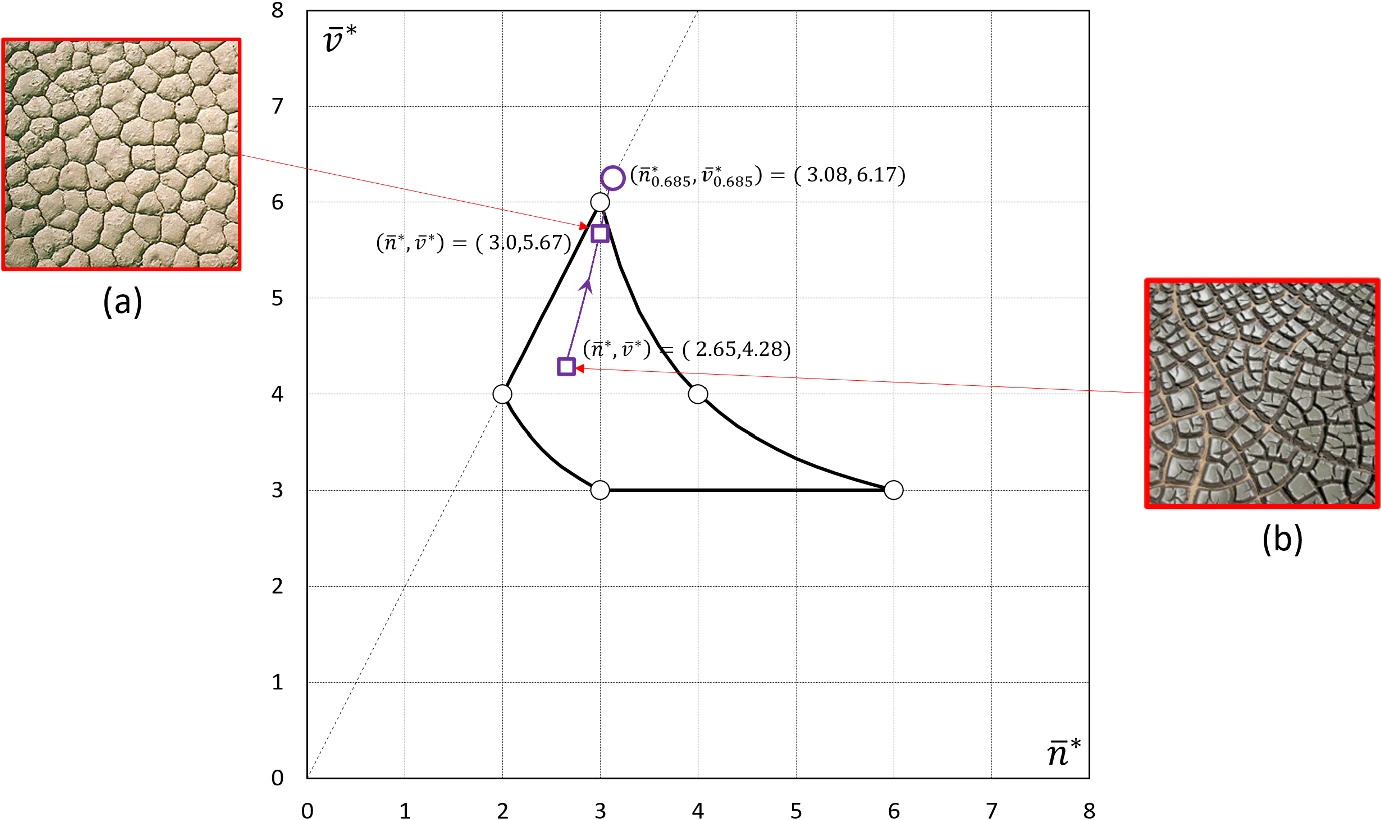
Abstract: We examine geological crack patterns using the mean field theory of convex mosaics. We assign the pair (n̅^∗, v̅^∗) of average corner degrees to each crack pattern and we define two local, random evolutionary steps R₀ and R₁, corresponding to secondary fracture and rearrangement of cracks, respectively. Random sequences of these steps result in trajectories on the (n̅^∗, v̅^∗) plane. We prove the existence of limit points for several types of trajectories. Also, we prove that cell density ρ̅=n̅^∗/v̅^∗ increases monotonically under any admissible trajectory.

On k-diametral point configurations in Minkowski spaces
Károly Bezdek, Zsolt Lángi

Abstract: The structure of k-diametral point configurations in Minkowski d-space is shown to be closely related to the properties of k-antipodal point configurations in ℝ^d. In particular, the maximum size of k-diametral point configurations of Minkowski d-spaces is obtained for given k≥2 and d≥2 generalizing Petty’s results on equilateral sets in Minkowski spaces. Furthermore, bounds are derived for the maximum size of k-diametral point configurations in given Minkowski d-space (resp., Euclidean d-space). Some of these results have analogues for point sets, which are discussed as well. In the proofs convexity methods are combined with volumetric estimates and combinatorial properties of diameter graphs.